202511131012 Status: idea Tags: Datascience, Machine Learning

linear regression

Linear regression is een Supervised learning methode. Het doel van Linear Regression is om een numerical target zoals bijvoorbeeld de prijs van een huis te voorspellen, dit doen we gebaseerd op input features zoals de grootte en de locatie.

De Basisformule

Lineaire regressie vindt de rechte lijn die het beste bij de data past. De formule voor deze lijn is:

$y^{\prime }=w\cdot x+b$

• $y^{\prime }$ (y-prime): Dit is de voorspelde waarde (de ‘numerical target’ die je probeert te vinden, bijvoorbeeld de voorspelde huisprijs).
• $x$: Dit zijn de features (de inputwaarden, zoals de grootte of locatie van het huis).
• $w$ (weights/gewichten): Dit zijn de gewichten. Ze bepalen de helling van de lijn en geven aan hoe belangrijk elke feature is voor de voorspelling.
• $b$ (bias/vertekening): Dit is de bias of het intercept (het snijpunt met de y-as). Het is de basiswaarde van de voorspelling als alle features $x$ nul zijn.

Kortom: De voorspelling $y^{\prime }$ is een combinatie van de inputfeatures $x$, waarbij elke feature een bepaald gewicht $w$ krijgt, plus een basiswaarde $b$.

Training van Lineaire Regressie

Het trainen van het model betekent het vinden van de beste waarden voor $w$ en $b$ zodat de lijn het dichtst bij alle datapunten ligt.

1. Meet Fouten: We vergelijken de voorspellingen $y^{\prime }$ met de werkelijke waarden $y$ (de actual values). Dit verschil noemen we de fout of het residu.
2. Gebruik een Loss Functie: Om de totale fout te meten, gebruiken we een Loss Functie. De meest voorkomende is de Mean Squared Error (MSE): $MSE=\text{gemiddelde van }(\text{voorspelling}-\text{werkelijkheid}{)}^2$
   • Waarom kwadrateren? Door het verschil te kwadrateren, wordt de fout altijd positief, en krijgen grote fouten een veel grotere straf, waardoor het model leert om ze te vermijden.
3. Minimaliseer het Verlies: Het doel van de training is om de gewichten ($w$) en de bias ($b$) zo aan te passen dat de MSE (loss) minimaal is. Dit minimaliseren van het verlies levert de ‘best-fit’ lijn voor de data op.

En dan heb ik hier nog een mooie visualisatie:

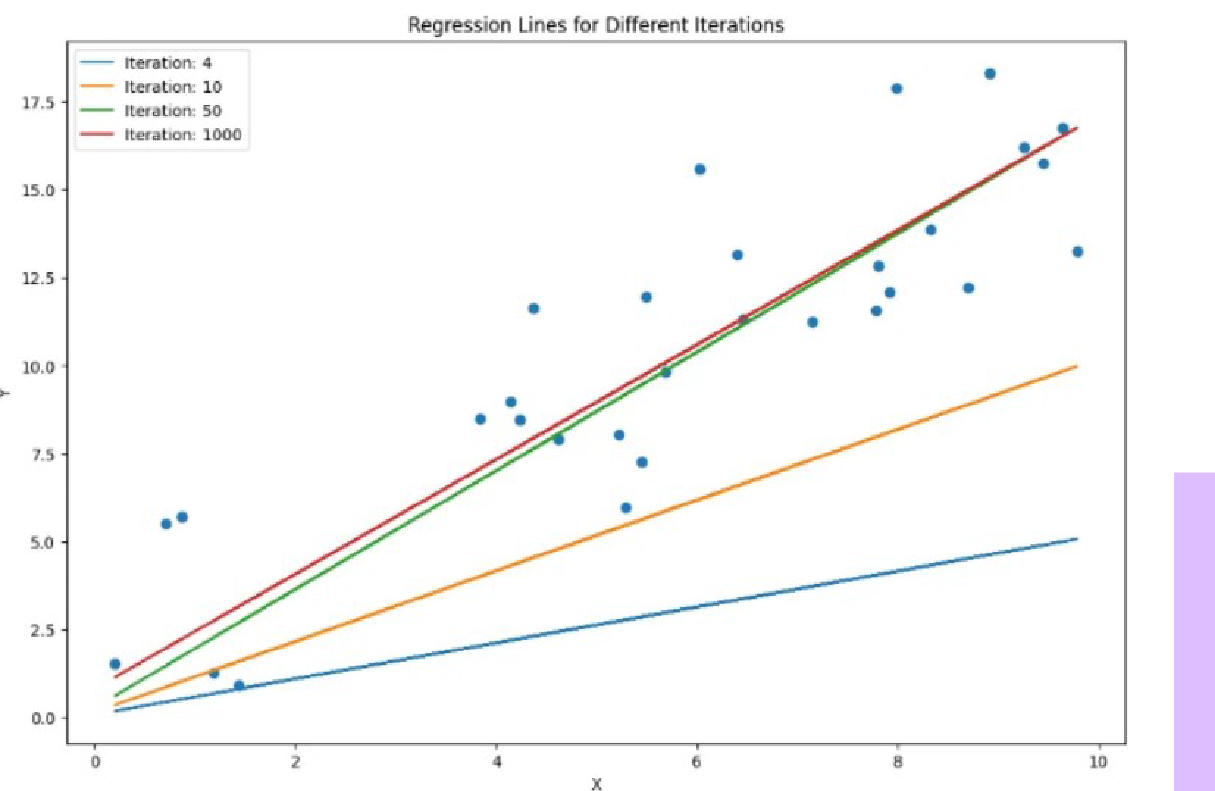
Hierbij kunnen we zien dat hoe meer iteraties, hoe meer de lijn in het midden ligt, en dat willen we.

---

References

Dit is iets wat we leren voor Datascience. dit was informatie vanuit avans 2-2 datascience 2025-11-10. en daarbij horen deze slides